Sommario
|
Operazioni preliminari all’analisi |
Il metodo degli elementi finiti |
Il metodo dell'equilibrio limite |
ll metodo delle strisce |
Metodo di Fellenius |
Metodo di Bishop |
Metodo di Janbu generalizzato |
Metodo di Morgenstern-Price |
Metodo di Bell |
Contributo stabilizzante di muri e paratie |
Riferimenti |
Un pendio, sia esso naturale o artificiale, può porsi in movimento, sotto l'effetto del peso proprio e di eventuali carichi esterni, dando luogo a fenomeni di tipo franoso che possono comportare pesanti conseguenze, sia dal punto di vista umano che economico. L'analisi di stabilità del pendio riguarda le relazioni che intercorrono tra le caratteristiche meccaniche del terreno che si oppongono al moto di scivolamento e le forze che invece tendono a provocarli. In questo articolo forniremo una introduzione alla problematica e le indicazioni operative utili per affrontare il problema con un software dedicato: ASPEN
L'analisi di stabilità globale presuppone generalmente i seguenti passi preliminari:
- Definizione del profilo longitudinale del pendio mediante rilievo della zona in esame.
- Definizione della stratigrafia mediante ingagini geofisiche e un sufficiente numero di sondaggi con prelievo di campioni indisturbati.
- Definizione delle caratteristiche fisiche e dei parametri di resistenza meccanica di ciascuna stratigrafia mediante prove di laboratorio sui campioni.
- Installazione di piezometri per determinare la presenza di falde e la loro escursione.
La stima della sicurezza
Definito così il contesto ed i parametri in gioco, l'analisi di stabilità del pendio si riconduce alla valutazione del coefficiente di sicurezza che il pendio offre rispetto all'insorgenza del movimento franoso ed alla previsione delle modalità cinematiche del moto di scivolamento. In questo contesto ha importanza una corretta definizione della superficie "critica" lungo cui avviene lo scivolamento.
Approcci di analisi
Sono fondamentalmente possibili due approcci di analisi, basati rispettivamente su una schematizzazione agli elementi finiti o su criteri di equilibrio limite.
Nel primo, che genericamente va sotto il nome di metodo degli elementi finiti, il pendio viene schematizzato come continuo elasto-plastico, dotato di opportuna legge di incrudimento che simuli il comportamento meccanico dei terreni.
La discretizzazione del pendio
L'intero pendio è discretizzato, suddiviso cioè in un reticolo relativamente fitto di piccoli elementi, all'interno dei quali l'andamento delle principali funzioni incognite (componenti dello spostamento e della tensione) è individuato dai valori che queste assumono nei vertici dell'elemento (nodi del reticolo di discretizzazione). Il comportamento del pendio può così ricondursi ad un sistema nonlineare di equazioni algebriche che, per quanto caratterizzato da un numero elevato di variabili (usualmente una discretizzazione accurata genera problemi dell'ordine delle diverse migliaia di variabili), può essere risolto per via numerica sfruttando la potenza di calcolo offerta dagli attuali calcolatori.
L’analisi incrementale
L'analisi è usualmente condotta per via incrementale, facendo crescere il carico esterno (o diminuendo la resistenza del terreno) mediante una successione di piccoli incrementi, fino al manifestarsi del fenomeno franoso. Risulta in genere estremamente onerosa e a volte di difficile interpretazione, per il gran numero di parametri coinvolti. Tuttavia, una corretta impostazione del metodo (definizione del legame costitutivo, tipo di elementi utilizzati, disposizione del reticolo di discretizzazione e conduzione della strategia incrementale) fornisce una valutazione accurata della sicurezza allo scivolamento, accompagnata da numerose altre informazioni relative allo stato di tensione e di deformazione che si sviluppa nel corso del fenomeno franoso.
Un approccio sensibilmente diverso è quello offerto dai cosiddetti metodi dell'equilibrio limite.
Caratteristica comune di questi è quella di ipotizzare la superficie di scivolamento lungo cui si svilupperà il moto franoso e quindi determinare il fattore di sicurezza del pendio attraverso un bilancio tra le forze attive, agenti sulla zona in movimento, e le forze resistive generate dalle tensioni presenti lungo la superficie di scorrimento. Essendo tale superficie, per ipotesi, in condizioni limite, le tensioni agenti sono direttamente ricavate dal criterio di collasso assunto per il terreno e quindi l'equilibrio globale della massa in frana può essere risolto in modo quasi immediato. Questo tipo di approccio è implementato nel software ASPEN
La superficie critica
L'analisi è quindi ripetuta a partire da una superficie di scivolamento diversa in modo da individuare per tentativi, fra tutte le ipotizzabili, la superficie critica caratterizzata dal valore del fattore di sicurezza più basso.
Ovviamente questa impostazione fornisce solo una risposta parziale al problema dell'analisi; non si hanno infatti informazioni (o si hanno informazioni solo parziali) degli andamenti delle tensioni e delle deformazioni agenti nel terreno. Tuttavia l'intero procedimento è molto snello e la soluzione fornita è in grado di caratterizzare gli aspetti più rilevanti del fenomeno franoso (fattore di sicurezza e superficie di scivolamento), presenta una buona affidabilità, è di facile interpretazione e contiene in se suggerimenti riguardo alla progettazione di eventuali interventi di consolidamento del pendio. Tutto ciò spiega l'ampia diffusione ed il favore che i metodi dell'equilibrio limite godono nella pratica corrente della professione.
Ipotesi di base dei metodi dell’equilibrio limite
L'analisi di stabilità condotta da ASPEN utilizza implementazioni relativamente sofisticate dei principali metodi dell'equilibrio limite, insieme ad algoritmi potenti di ricerca automatica della superficie critica. Ciò consente di ottenere risultati affidabili in termini di fattore di sicurezza e di andamento della superficie di scivolamento.
L’ipotesi di stato di deformazione piano
Si deve tener presente tuttavia che il pendio è analizzato in condizioni di deformazione piana e quindi prescindendo dal contesto tridimensionale in cui è inserito. Questa semplificazione facilita notevolmente sia la descrizione geometrica del piano di campagna e della stratigrafia, sia l'esecuzione dell'analisi, in quanto consente di operare con superfici cilindriche riconducibili a curve nel piano. Si deve tener presente, tuttavia, che uno stato di deformazione piana rappresenta il fenomeno franoso solo nelle zone centrali di frane aventi forma approssimativamente cilindrica, molto allungata in direzione ortogonale al piano di deformazione. Tale situazione non si verifica tuttavia facilmente, data l'anisotropia del materiale, la forma quasi sempre irregolare del pendio, la presenza di superfici di discontinuità, l'andamento delle pressioni neutre e tutte le altre irregolarità in concreto presenti. Se tutto ciò conduce, in genere, ad una sotto stima del reale fattore di sicurezza non possono comunque escludersi casi isolati in cui il fattore ricavato in funzione dell'ipotesi di deformazione piana sia localmente sovrastimato rispetto al reale comportamento tridimensionale. Pertanto i risultati prodotti da ASPEN devono essere accompagnati da una discussione che affronti il prevedibile aspetto tridimensionale del fenomeno franoso.
Criterio di Mohr-Coulomb
Posizione base dei metodi di equilibrio limite è che, in condizioni di incipiente scivolamento la tensione tangenziale tf agente sulla superficie di scivolamento in opposizione al movimento sia espressa dalla formula di Mohr-Coulomb:
tf = c' + (sn - uw) tg f'
in cui:
c' è la coesione in termini di pressioni effettive,
sn è la pressione normale totale,
uw è la pressione neutra,
f' è l'angolo di attrito interno.
Le quantità c' e f' sono ovviamente caratteristiche del terreno attraversato mentre sn e uw dipendono dalla soluzione considerata.
L'applicazione di un fattore di sicurezza F > 1 fa si che nella impostazione dell'equilibrio ci si riferisca alla tensione ridotta:
tf = (c' + (sn - uw) tg f') / F
Sarà questa la tensione resistiva da considerare nell'equilibrio della massa in frana.
In linea più generale il coefficiente di sicurezza può essere differenziato per i contributi di coesione e di attrito.
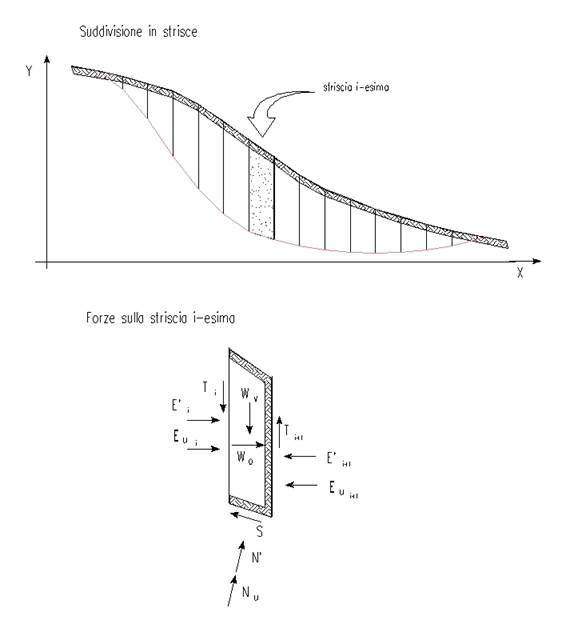
Per tener conto in modo semplice ma sufficientemente accurato dell'andamento variabile delle tensioni lungo la superficie di scivolamento, l'intero pendio viene suddiviso in un insieme opportunamente fitto di strisce verticali come indicato in figura.
Le forze agenti sulla striscia
La generica striscia è sottoposta ad un sistema di forze derivanti dalle azioni interne (peso proprio ed eventuale carico sismico) e dalle azioni di contatto agenti sul piano di campagna, sulle due interfacce (di sinistra e di destra) che la collegano alle strisce adiacenti e sulla parte della superficie di scivolamento che interseca la striscia.
Con riferimento alla figura ed assumendo uno spessore trasversale unitario, possiamo distinguere:
· Wv Carico verticale totale sulla striscia (peso proprio, carichi agenti sul piano di campagna ed eventuali altre forze note);
· Wo Carico orizzontale totale (azione sismica, effetto di tiranti ed altro);
· E' Risultante delle tensioni normali effettive sull'interfaccia:
· Eu Risultante delle tensioni neutre sull'interfaccia;
· T Risultante delle tensioni tangenziali sull'interfaccia;
· N' Risultante delle tensioni normali effettive agenti lungo la superficie di scivolamento;
· Nu Risultante delle tensioni neutre agenti lungo la superficie di scivolamento;
· S Risultante delle tensioni tangenziali agenti lungo la superficie di scivolamento.
I termini noti
Le risultanti dei carichi Wv e Wo,e le risultanti delle tensioni neutre Eu ed Nu sono in generale note sia in intensità che in posizione (sono infatti o direttamente definite o facilmente calcolabili dai dati del problema).
I termini incogniti
Tutte le altre sono da considerare incognite sia in termini di intensità che di posizione. Per l'intero pendo, che pensiamo suddiviso in n strisce, abbiamo così le seguenti variabili:
· n-1 risultanti normali E' agenti sulle (n-1) interfacce;
· n-1 risultanti tangenziali T agenti sulle (n-1) interfacce;
· n risultanti normali N' agenti sulle n intercette della superficie di scivolamento;
· n risultanti tangenziali S agenti sulle n intercette della superficie di scivolamento;
· n-1 ascisse di applicazione delle forze orizzontali E';
· n ascisse di applicazione delle forze normali N';
· 1 fattore di sicurezza F del pendio.
per un totale quindi di (6n - 2) incognite.
Le equazioni disponibili
D'altra parte, per ciascuna delle n strisce del pendio, possiamo scrivere tre equazioni di equilibrio di corpo rigido (in direzione orizzontale, verticale ed alla rotazione) ed una condizione di Mohr-Coulomb.
Il problema sotto determinato
Il problema, così caratterizzato da 4n equazioni e (6n-2) incognite, risulta ovviamente sottodeterminato e richiede pertanto (2n-2) assunzioni indipendenti per poter essere risolto in modo univoco.
Le assunzioni dei vari metodi
La maggior parte dei metodi dell'equilibrio limite assume come noto il punto di applicazione della forza normale N agente alla base della striscia (generalmente posizionato nel punto medio). In tal modo restano ancora n-2 assunzioni da effettuare. Un modo semplice di introdurre ulteriori assunzioni è quello di definire la posizione delle forze orizzontali di interfaccia E' (come nel metodo di Janbu) od il rapporto T/E' tra le forze verticali ed orizzontali di interfaccia (come nei metodi di Bishop e di Spencer).
Metodi parzialmente equilibrati
Ciò conduce però ad un totale di (n-1) assunzioni e pertanto rende sovradeterminato il problema: diventa cioè impossibile verificare contemporaneamente tutte le equazioni di equilibrio del problema di cui almeno una viene ad essere ignorata (ad esempio l'equazione globale alla traslazione orizzontale nel metodo di Bishop o quella alla rotazione globale nel metodo di Janbu).
Metodi totalmente equilibrati
Metodi totalmente equilibrati, che verificano cioè tutte le equazioni del problema, possono essere ottenuti introducendo un ulteriore parametro incognito che permetta di pareggiare il numero di equazioni e di incognite.
I vari metodi per l'analisi di stabilità dei pendii disponibili in letteratura, a parte differenze di dettaglio relative al modo con cui sono calcolate le varie quantità in gioco o al modo in cui viene condotta la sequenza iterativa necessaria alla soluzione del problema, si differenziano sostanzialmente per il numero e tipo di assunzioni operate, come mostrato in tabella.
| METODO |
ASSUNZIONI OPERATE |
EQUILIBRI MANCANTI: |
| Fellenius |
Non sono considerate le forze di interstriscia |
rotazione |
| Bishop |
Si assumono nulle i tagli di interstriscia |
traslazione |
| Janbu |
Viene definita la posizione delle forze orizzontali di
interstriscia E in funzione dell'altezza totale del concio
|
rotazione |
| Spencer |
La risultante delle forze di interstriscia ha pendenza
costante lungo tutta la massa scivolante
|
Traslazione
o rotazione |
Morgenstern
Price |
La direzione della risultante delle forze di interstriscia è definita usando una funzione arbitraria |
nessuno |
| Bell |
Viene ipotizzata la distribuzione delle tensioni normali sulla superficie di scivolamento |
nessuno |
| Maksumovic |
Come Morgenstern-Price. Differisce per il calcolo dei carichi esterni,
per lo schema iterativo ed altri dettagli.
|
nessuno |
|
Sarma
|
Come Morgenstern--Price. Differisce per la definizione del fattore di sicurezza che è assunto come moltiplicatore delle forze orizzontali esterne.
|
nessuno
|
I metodi di tipo totalmente equilibrato, come quello di Morgenstern-Price, risultano ovviamente di utilizzo più complesso ma sono allo stesso tempo più accurati ed affidabili.
I metodi disponibili in ASPEN
Il programma ASPEN contiene una implementazione, per certi versi sofisticata, dei seguenti metodi:
Come si vede, accanto al metodo di Morgenstern-Price, che sarà in generale da preferirsi nell'analisi, sta inserita una ampia selezione di altri metodi, scelti tra quelli più diffusi nella pratica professionale, in modo da facilitare il confronto con risultati ottenuti per via diversa.
Fra questi, il metodo di Fellenius è senz'altro il più semplice ma anche il meno accurato
I metodi di Bishop e di Janbu rappresentano entrambi metodi classici ma ancora di amplissima diffusione.
Dei metodi totalmente equilibrati più recenti è stato inserito il solo metodo di Bell in quanto è il solo ad utilizzare assunzioni sensibilmente diverse da quello di Morgenstern-Price.
L'applicazione dei diversi metodi porta in generale a valutazioni diverse del fattore di sicurezza F (come dicevamo i risultati forniti dal metodo di Morgenstern-Price sono comunque da ritenersi più accurati). Tuttavia, a parte il metodo di Fellenius che, come noto, può condurre ad una forte sopravalutazione di F, le differenze sono usualmente contenute nell'ordine del 1%.
Il metodo è stato proposto da Fellenius nel 1936 con riferimento a frane con superficie di scivolamento circolare ed è noto anche come metodo ordinario o metodo svedese. Rappresenta in qualche modo il precursore dei metodi delle strisce e si basa sull'ipotesi semplificativa che la forza risultante di interfaccia (composizione della forza normale E e tangenziale T) agisca parallelamente al tratto di superficie di scivolamento posta a base della striscia. In tali condizioni, la forza normale N agente sulla base della striscia può essere ricavata dall'equilibrio della striscia, in funzione dei soli carichi esterni. Nota N, la forza tangenziale di base S deriva come diretta conseguenza della condizione di Mohr-Coulomb:
S = L c' + (N - Nu) tg f
Imponendo l'equilibrio globale del corpo in frana (alla rotazione) si ottiene una formula esplicita molto semplice che fornisce direttamente il fattore di sicurezza cercato F.
Il metodo è senz'altro molto semplice e rapido; tuttavia porta generalmente ad una sopravvalutazione, a volte grossolana, del fattore di sicurezza e deve quindi essere considerato poco affidabile. La sua utilizzazione dovrebbe pertanto essere limitata a soli fini di confronto. La versione implementata in ASPEN resta comunque molto accurata nel calcolo delle forze in gioco ed è, per il modo in cui è implementata, applicabile anche nei casi di superfici di scivolamento non circolari ed in presenza di azioni (sismiche o di altra origine) orizzontali.
Il metodo, meglio noto come metodo semplificato di Bishop, è stato proposto nel 1955 in relazione a frane con superficie di scivolamento circolare. L'ipotesi da cui parte è che la risultante delle forze di interfaccia sia orizzontale (che cioè sia nulla la forza tangenziale di interfaccia T). Su questa base, l'equilibrio globale alla rotazione del corpo in frana porta ad una formula in F appena più complicata di quella di Fellenius. Tuttavia la formula si presenta implicita, cioè il fattore di sicurezza compare in entrambi i membri dell'equazione, e pertanto deve essere risolta per iterazione. Ciò comporta una inevitabile maggiore complessità computazionale anche se lo schema iterativo utilizzato risulta rapidamente convergente.
Malgrado che il metodo non risulti totalmente equilibrato, non assicura infatti (esattamente) l'equilibrio globale in direzione orizzontale, le equazioni in gioco restano comunque agevoli e l'errore commesso con comporta forti errori nella valutazione finale del fattore di sicurezza. Ciò rende il metodo affidabile nella pratica professionale e ne spiega la grande diffusione.
L'implementazione contenuta in ASPEN usa un calcolo molto accurato delle forze in gioco insieme ad una scrittura delle equazioni che ne rendono possibile l'applicazione anche in casi di superfici di scivolamento non circolari ed in presenza di azioni orizzontali. Si tenga presente tuttavia che per superfici di scivolamento molto diverse dalla forma circolare, il mancato rispetto dell'equilibrio in direzione orizzontale può comportare un incremento di errore.
Il metodo, noto anche come metodo generalizzato delle strisce, è stato sviluppato nel corso degli anni '60 da Janbu come metodo semplice utilizzabile per frane con superficie di scivolamento del tutto generica.
Il metodo usa una impostazione simile a quella di Bishop, tuttavia utilizza una diversa ipotesi base. È infatti considerata nota la posizione della risultante normale di interstriscia E, in generale assunta pari ad 1/3 dell'altezza complessiva della striscia. Le equazioni di equilibrio delle strisce sono riscritte in modo da assicurare esattamente l'equilibrio globale alla traslazione orizzontale e verticale, ma solo in modo approssimato l'equilibrio alla rotazione. Si ottiene anche in questo caso una formula implicita da risolvere per iterazione.
Il metodo è di applicazione semplice ed ampiamente diffuso nella pratica. Fornisce in generale risultati abbastanza affidabili, anche se è caratterizzato da una tendenza alla sottovalutazione del fattore di sicurezza e da una risposta non precisa (ed a volte oscillante) della curva delle pressioni.
L'implementazione contenuta in ASPEN si differenzia dalla versione standard del metodo (vedi ad esempio il testo di Bromhead già citato nei Riferimenti) per un calcolo molto accurato delle forze in gioco e per l'uso di uno schema iterativo differente da quello proposto inizialmente da Janbu. Lo schema iterativo originale infatti, anche se porta ad una rapida convergenza iniziale, tende a rallentarla o perderla del tutto nella fase successiva del ciclo iterativo.
Il metodo, sviluppato da Morgenstern, Price ed altri autori inglesi dell'Imperial College nella seconda metà degli anni '60, assume la sola ipotesi che il rapporto T/E, tra le forze verticali ed orizzontali di interstriscia, sia esprimibile attraverso una funzione incognita i cui parametri sono ricavati dall'equilibrio globale del corpo in frana. Diviene così possibile definire una soluzione totalmente equilibrata, che rispetta cioè tutte le equazioni di equilibrio del problema; tuttavia il metodo non conduce ad una formula finale semplice, come nei metodi precedenti, ma ad un sistema di equazioni nonlineari da risolvere mediante uno schema iterativo alla Newton-Rapshon e risulta pertanto sensibilmente più complesso ed oneroso.
Il metodo resta comunque caratterizzato da una elevata accuratezza ed affidabilità e viene assunto come riferimento in tutti i metodi successivi che propongono solo differenze di dettaglio, spesso originate da sole esigenze di semplificazioni di calcolo. La sua maggiore complessità ne ha tuttavia limitato la diffusione nella pratica professionale.
L'implementazione contenuta in ASPEN è caratterizzata da un calcolo molto accurato delle forze in gioco e da alcune varianti nello schema iterativo di soluzione che ne migliorano sensibilmente l'affidabilità numerica e la velocità di esecuzione.
Il metodo, proposto da Bell nel 1968 segue una via in qualche modo diversa in quanto, a differenza dei precedenti, si basa direttamente sull'equilibrio globale dell'intera massa in frana. La suddivisione in conci viene utilizzata unicamente per comodità di calcolo e per determinare con maggior precisione, mediante sommatoria, le forze in gioco e l'indeterminazione statica è superata formulando una ipotesi sull'andamento delle tensioni normali agenti lungo la linea di scivolamento (viene assunta una distribuzione sinusoidale).
Per come è formulato, il metodo risulta totalmente equilibrato (sono cioè esattamente verificate tutte e tre le equazioni di corpo rigido della massa in frana). Malgrado ciò, l'insieme delle equazioni in gioco si presenta semplice ed un accorgimento numerico (trattare cioè la coesione c' come variabile incognita) ne permette una agevole soluzione per via iterativa. Per tali motivi rappresenta un ottimo compromesso fra accuratezza e rapidità di esecuzione.
L'implementazione contenuta in ASPEN si caratterizza per il calcolo accurato delle forze in gioco, anche se conserva in pieno le equazioni base e lo schema iterativo originale del metodo.
I muri e le paratie posizionati sul pendio danno un contributo alla stabilità in quanto in linea generale producono
- un contributo di attrito sulla superficie di scivolamento per effetto del loro peso proprio;
- un contributo di spinta per effetto dell’interazione opera e terreno in movimento.
Contributo di attrito
Se la la superficie di scorrimento non interseca l’intervento, il contributo stabilizzante è unicamente dovuto all’incremento della tensione tangenziale di attrito. Infatti, per effetto del peso proprio dell’intervento si ha un incremento ΔN della forza normale agente sulla base della striscia, e quindi un incremento Δtf della tensione tangenziale pari a:
Δtf = ΔN tg φ
Contributo di spinta
Nel consolidamento di pendii sono frequentemente usati interventi strutturali, come muri e paratie, capaci di intercettare forze instabilizzanti all’interno del corpo in frana e trasferirle al sostrato stabile, posto al di sotto della superficie di scivolamento. Se la superficie di rottura non interseca l’opera, il meccanismo di interazione non si crea e non si ha nessun contributo di spinta.
Se invece l’opera attraversa tutta la massa in movimento e raggiunge il terreno stabile al di sotto della superficie di rottura, per effetto degli spostamenti orizzontali del terreno, si desta sull’opera una spinta dovute alle forze laterali trasmesse dal terreno. La valutazione di queste forze riconduce allo studio dell’interazione fra opera e pendio in frana ed è un problema affrontato da diversi autori (Broms, Viggiani, Ito & Matsui, De Beer & Carpenter, Fukuoka, Poulos, et al.).
Nel presente programma si propone una metodoligia di valutazione della spinta basata sull’analisi dei meccanismi di collasso locale che tipicamente possono verificarsi in queste situazioni, con riferimenti ai lavori teorici degli autori sopracitati.<p >In particolare sono considerati le quattro situazioni limite:
- crisi da scorrimento dell’opera,
- crisi da ribaltamento dell’opera,
- crisi da rottura del fronte spingente,
- crisi da tranciamento dell’opera,
che consentono di stimare con buona approssimazione valori limiti superiori della spinta offerta dall’intervento, in opposizione allo scorrimento del pendio.
Il valore di calcolo della spinta, cioè il valore realmente messo in conto nell’analisi, si assume infine come il valore minore registrato nei quattro casi limite, opportunamente ridotto mediante il coefficiente di sicurezza fsic assegnato in input, per l’opera in esame.
In particolare, la spinta di calcolo S si ottiene dalla seguente relazione:
S = min(Sls, Slr, Slf, Slt)/fsic
in cui
Sls è la spinta limite di scorrimento,
Slr è la spinta limite di ribaltamento,
Slf è la spinta limite di rottura fronte,
Slt è la spinta limite di tranciamento.
Le ipotesi semplificative adottate nell’analisi di tali meccanismi di crisi si accordono col livello delle approssimazioni insite in tutto il processo di modellazione e di analisi, di cui si è già discusso nei paragrafi precedenti. Si suppone, in particolare, che la spinta offerta dall’intervento strutturale sia orizzontale e applicata ad un terzo dell’altezza utile del fronte di spinta. Altre ipotesi sono assunte per le distribuzioni tensionali nell’intorno dell’intervento, assumendo andamenti costanti o lineari, corrispondenti a condizioni di plasticizzazione o a situazioni di spinta passiva esprimibili secondo la formula di Rankine o di Bell.
Contributo di spinta per i muri di sostegno
Analizziamo con maggiore dettaglio le situazioni limite di lavoro per il caso dei muri di sostegno.
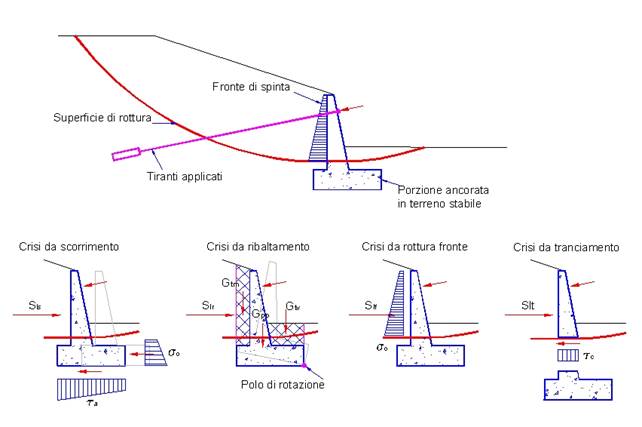
Meccanismo di crisi da scorrimento
Nel meccanismo di crisi da scorrimento si suppone che alla base del muro di sostegno siano mobilitate delle tensioni tangenziali di attrito e una distribuzione di tensioni orizzontali sul fronte di valle della porzione ancorata in terreno stabile. Le tensioni tangenziali di attrito alla base del muro di sostegno si suppongono distribuite con legge lineare e sono valutate in funzione delle tensioni effettive presenti agli spigoli di monte e di valle.
La distribuzione di tensioni orizzontali sul fronte di valle, anch’essa espressa con legge lineare, è valutata applicando la formula di Bell per il caso di spinta passiva:
so = sv tg2(45+f/2) + 2c tg(45+f/2)
La spinta Sls corrispondente al meccanismo di crisi per traslazione si ottiene quindi dall’equilibrio orizzontale con le forze resistenti, che in particolare sono la risultante delle tensioni tangenziali di attrito, la risultante delle tensioni passive orizzontali sul fronte valle e l’azione dei tiranti applicati.
Meccanismo di crisi da ribaltamento
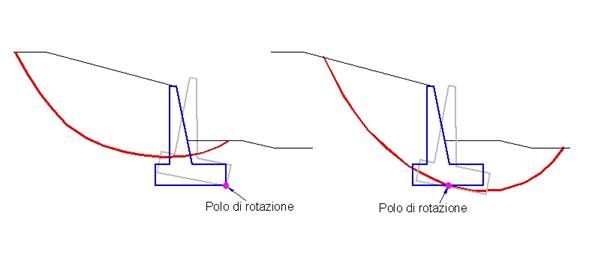
La spinta utile Slr per questo meccanismo di crisi si ottiene dall’equilibrio alla rotazione fra le forze agenti sul muro di sostegno. Interviene in particolare il peso proprio del muro di sostegno, le azioni dei tiranti applicati e il peso del terreno gravante sulla suola di fondazione. Il polo di rotazione si assume coincidente con lo spigolo inferiore di valle della porzione di muro di sostegno collocata in terreno stabile. Se la superficie di rottura dovesse tagliare la suola di fondazione, il polo di rotazione arretra verso monte e si posiziona sulla linea di taglio con la superficie di rottura.
Meccanismo di crisi da rottura fronte
La spinta utile Slf è definita da meccanismi di crisi che si possono verificare sul fronte dell’opera direttamente investito dalla massa in scivolamento. Nel caso del muro di sostegno questa viene valutata come risultante delle tensioni orizzontali agenti sul fronte, nell’ipotesi di stato passivo.
Meccanismo di crisi da tranciamento
La spinta utile Slt al limite del tranciamento si ottiene valutando l’area della sezione di muro di sostegno tagliata dalla superficie di rottura e supponendo che su tale area si mobiliti la tensione tangenziale di rottura, caratteristica del materiale che costituisce il muro di sostegno.
Contributo di spinta per le paratie
In maniera analoga al caso dei muri, anche per le paratie la spinta stabilizzante di calcolo viene valutata considerando quattro diversi meccanismi semplificati di collasso, corrispondenti a possibili situazioni di crisi dell’opera, ed assumendo come spinta di calcolo S il valore minimo, ulteriormente ridotto tramite il coefficiente di sicurezza assegnato.
Analizziamo con maggiore dettaglio le situazioni limite di lavoro per il caso delle paratie.
Paratie continue e discontinue
I valori meccanici che intervengono nel calcolo, come i pesi o la spinta resistente, sono sempre riferiti alla striscia di pendio di larghezza unitaria (1 metro). Nel caso di paratia discontinua, costituite da pali posti ad un determinato interasse, interviene quindi un fattore riduttivo fri che tiene conto della densità dei pali in direzione ortogonale alla sezione stratigrafica.
Meccanismo di crisi da scorrimento
Nel meccanismo di crisi da scorrimento si suppone che alla base della paratia siano mobilitate delle tensioni tangenziali di attrito e una distribuzione di tensioni orizzontali sul fronte di valle della porzione ancorata in terreno stabile. Le tensioni tangenziali di attrito alla base della paratia si suppongono distribuite con legge lineare e sono valutate in funzione delle tensioni effettive presenti agli spigoli di monte e di valle.
La distribuzione di tensioni orizzontali sul fronte di valle, anch’essa espressa con legge lineare, è valutata applicando la formula di Bell per il caso di spinta passiva:
so = sv tg2(45+f/2) + 2c tg(45+f/2)
La spinta Sls corrispondente al meccanismo di crisi da scorrimento si ottiene quindi dall’equilibrio orizzontale con le forze resistenti, che in particolare sono la risultante delle tensioni tangenziali di attrito, la risultante delle tensioni passive orizzontali sul fronte valle e l’azione dei tiranti applicati.
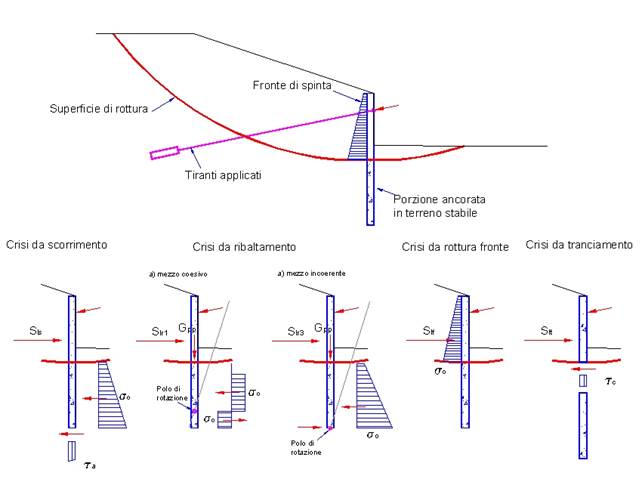
Meccanismo di crisi da ribaltamento
La spinta utile Slr per questo meccanismo di crisi si ottiene dall’equilibrio alla rotazione fra le forze e le tensioni del terreno agenti sulla paratia. Si utilizza in questo caso la teoria del Broms, basata sull’applicazione dei teoremi dell’analisi limite, nell’ipotesi che il palo sia libero di ruotare in testa e supponendo che la crisi sopravvenga per la plasticizzazione del terreno, piuttosto che per rottura strutturale (meccanismo di palo corto). Intervengono nel bilancio il momento della spinta, applicata ad un terzo del fronte di spinta, il momento delle forze dovute ai tiranti e il momento delle tensioni orizzontali, che si sviluppano lungo il fusto infisso in terreno stabile.
Vengono trattati separatamente i casi di mezzo puramente coesivo e di mezzo incorente e si assume come spinta limite il risultato maggiore fra i due casi, cioè:
Slf = max(Slr1, Slr2)
in cui
Slr1 è la spinta limite considerando il solo contributo coesivo,
Slr2 è la spinta limite considerando il solo contributo d’attrito.
Caso del mezzo puramente coesivo
In questo caso, il Broms fa l’ipotesi, confortata da risultanze sperimentali, che la reazione del terreno, in condizioni limite, sia nulla fino alla profondità di 1,5 B e poi costante con valore pari a 9cuB, in cui B è il diametro del palo e cu è la coesione non drenata. Il polo di rotazione si assume posto ad una certa profondità. Il palo ruota rigidamente attorno a tale punto, producendo un campo tensionale limite come quello riportato in figura.
Dagli equilibri alla traslazione ed alla rotazione si possono ricavare le incognite del problema, fra cui il valore della spinta limite.
Caso del mezzo puramente incoerente
In questo caso, il Broms fa l’ipotesi che la reazione del terreno, in condizioni limite, sia nulla al piano campagna e crescente linearmente con la profondità, con la legge 3Kpgz. In pratica questa distribuzione corrisponde alla spinta passiva di Rankine, amplificata con un fattore 3, per compensare le ipotesi semplificative insite nell’assunzione del coefficiente Kp.
Si ipotizza, inoltre, che il polo di rotazione coincida con la punta del palo. Questa assunzione si verifica con buona approssimazione e consente di semplificare il problema sostituendo alla reazione distribuita al di sotto del punto di rotazione una forza concentrata passante per la base del palo. In queste condizioni, il valore della spinta limite si può ricavare dal solo equilibrio alla rotazione.
Meccanismo di crisi da rottura fronte
La spinta utile Slf è definita da meccanismi di crisi che si possono verificare sul fronte dell’opera direttamente investito dalla massa in scivolamento. Per le paratie continue la valutazione della spinta è analoga a quelle per i muri. Nel caso di paratie discontinue, si assume la teoria di Broms per la fila di pali, che tiene conto della possibilità di rottura del terreno compreso fra due pali e quindi dell’inefficacia progressiva dell’effetto arco al crescere dell’interasse. In ogni caso la spinta è sempre limitata dal valore limite ottenibile sulla paratia continua, dove comanda la rottura del terreno a monte.
Meccanismo di crisi da tranciamento
La spinta utile Slt al limite del tranciamento si ottiene valutando l’area della sezione di paratia tagliata dalla superficie di rottura e supponendo che su tale area si mobiliti la tensione tangenziale di rottura, caratteristica del materiale che costituisce la paratia.
Come si è accennato, i metodi dell'equilibrio limite presuppongono una serie di ipotesi semplificative sul comportamento del pendio, ed in particolare sull'andamento delle forze di interstriscia, che, se pure possano in molti casi apparire ragionevoli, è comunque bene tener sempre presenti nell'interpretazione dei risultati. Per una migliore comprensione dei diversi metodi si consiglia la lettura dei lavori originali dei diversi autori, qui di seguito elencati:
· Fellenius W., Calculation of the stability of earth dams, Trans. 2nd Congress on Large Dams, Washington, 1936, p. 445.
· Bishop A. W., The use of the slip circle in the stability analysis of earth slopes, Geotechnique, vol. 5, pp. 7--11, 1955.
· Bell J. M., General slope stability analysis, J. Soli Mech. and Foundation Div., ASCE, nov. 1968.
· Janbu N., Slope stability computation, Embankment Dam Engineering, Casagrande Volume, pp. 47--86, 1973.
· Morgenstern N. R. , Price V. E., The analysis of stability of general slip surfaces, Geotechnique, vol. 15, pp. 79--93, 1965.
· Morgenstern N. R., Price V. E., A numerical method for solving the equations of stability of general slip surfaces, The Computer Journal, vol. 9, pp. 388--393, 1967.
· Broms B.B., Lateral resistance of piles in cohesive soil, J. Soil Mech. Founf. Div. ASCE SM2, pp. 27-63, 1964.
· Broms B.B., Lateral resistance of piles in cohesionless soil, J. Soil Mech. Founf. Div. ASCE SM3, pp. 123-156, 1964.
· Broms B.B., Earth pressures on piles in a row due to lateral soil movement, Soils and Foundations, vol.23, n.3, 1983.
· Ito T., Matsui T., Hong W.P., Design method for stabilizing piles against landslide, one row of piles, Soils and Foundations, vol. 21, n.1, 1981
Utili per approfondire l'argomento e di facile reperibilità risultano i seguenti testi:
· Lambe T. W., Whitman R. V., Soil Mechanics - SI version, Wiley, Singapore, 1979.
· Bromhead E. N. , Stabilità dei pendii, Flaccovio Editore, Palermo, 1986.