NOVITA' DELLA VERSIONE EDIPLIN 3.0
Analisi e verifiche di plinti su pali o superficiali in c.a.
La nuova versione Ediplin 3.0 si allinea alle ultime Norme Tecniche per le Costruzioni italiane (Ntc18) ed apre agli EuroCodici, ampliando di fatto l'area di applicabilità del programma su scala internazionale. Nel contempo il programma viene arricchito di nuove funzionalità che ne estendono la capacità di modellazione e ne aumentano le prestazioni, come illustreremo brevemente in questa scheda.
Nuovi sistemi normativi disponibili
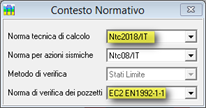
Il programma prevede adesso due nuove opzioni per la norma tecnica di calcolo: le Ntc18 italiane e gli EuroCodici. Come norma di dettaglio per i pozzetti è stato aggiunto l'EuroCodice 2, che introduce le tecniche di verifiche basate sui modelli “strut & tie”, raccomandati anche dalle Ntc18 (§. 8.4) per il progetto di elementi tozzi, di zone diffusive e delle regioni con forti discontinuità geometriche e di carico (nodi, supporti).
La scelta del sistema normativo si può effettuare con l'opzione di menù Dati | Contesto normativo.
Generalizzazione degli stati limite di verifica
Per consentire l'utilizzo in differenti contesti normativi, la definizione e la gestione degli stati limite di verifica è stata riorganizzata e resa più efficiente e generale. Sono adesso disponibili due tabelle di definizione: la prima riguardante i fattori di combinazione delle azioni, la seconda i fattori di sicurezza da assumere sui materiali e le opzioni per l'attivazione delle verifiche.
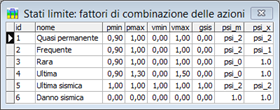
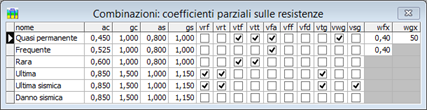
Si tenga presente, che il programma provvede ad impostare i valori e le opzioni secondo le indicazioni della normativa selezionata, per cui non sono in genere richiesti interventi diretti dell'utente nelle due griglie riportate in figura. Eventuali impostazioni autonome sono riservate per un uso esperto, per definire contesti normativi non ancora contemplati esplicitamente nel programma o per trattare casi particolari: ad esempio per considerare fattori più restrittivi o per attivare una particolare verifica su stati limite in cui, secondo norma, non sia strettamente necessaria.
Analisi per carichi già combinati
Nella versione attuale è stata prevista la possibilità di definire i carichi agenti, oltre che per singola azione (come nella versione precedente), anche per azioni combinate.
Nella pratica progettuale può capitare che il fornitore o il costruttore della sovrastruttura da realizzare sul plinto (sia essa una pala eolica, un traliccio o una pila da ponte) non fornisca il dettaglio dei carichi per singola azione, ma combinazioni di carico già predisposte per alcuni stati limite di riferimento, in uno o più casi di inviluppo. In questi casi si lavora quindi con carichi già combinati, l'analisi è eseguita per ogni scenario di carico e le sollecitazioni di verifica sono direttamente quelle ottenute dalle analisi eseguite.
Nella versione precedente, una situazione del genere costituiva un serio ostacolo perché il programma non consentiva l'immissione dei carichi già combinati e, se non c'erano altre alternative, era necessaria una operazione di disassemblaggio del carico combinato per ottenere le componenti per singola azione da assegnare nel programma. Ora questo non è più necessario perché la definizione dei carichi è stata estesa anche ai carichi combinati. In particolare l'utente può:
1. assegnare solo le componenti di carico per singola azione, lavorando come nella versione precedente,
2. assegnare le componenti di carico per singola azione e in aggiunta i carichi combinati che desidera considerare,
3. non assegnare carichi per singola azione, lavorando solo con carichi già combinati.
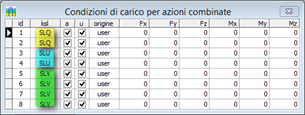
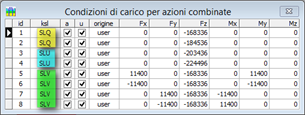
Nelle figure è mostrata la griglia di definizione dei carichi combinati: nella fase iniziale, prima che vengano definiti i valori di carico nei pilastri, e nella fase finale dopo che tale operazione sia conclusa.
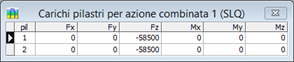
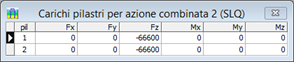
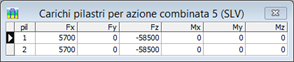
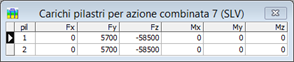
Per ogni caso di carico definito devono quindi essere inseriti i valori numerici delle componenti
(forze Fx, Fy, Fz e coppie Mx, My e Mz), supposte agenti alla base di ogni pilastro.
Per i carichi assegnati come singola azione, la procedura prevede l'analisi dei singoli casi e poi l'inviluppo delle sollecitazioni con le leggi di combinazione previste per ogni stato limite.
Il progetto del pozzetto secondo i modelli strut & tie
Nelle versioni precedenti il progetto e la verifica del pozzetto faceva riferimento alle norme italiane C.N.R.10025, nelle due versioni del 1984 e del 1998, che all'epoca rappresentavano le fonti normative più esaurienti per la tipologia in esame. Negli anni successivi, gli EuroCodici hanno inquadrato la materia nell'ambito più generale dei problemi con forti discontinuità geometriche o di carico, come ad esempio succede per le travi alte, le mensole tozze, i plinti su pali ed altre strutture di supporto, fra cui i pozzetti per l'alloggiamento di pilastri. In queste regioni la distribuzione delle tensioni e delle deformazioni assume un carattere nonlineare e decade il principio di De Saint Venant, l'ipotesi di conservazione delle sezioni piane e l'applicabilità stessa della teoria tecnica della trave. Per ovviare a questo deficit, viene in soccorso il metodo STM (Strut & Tie Methods), che trae origine dai lavori di W. Ritter (1899) e E. Mörsch (1912) per il progetto a taglio delle travi in c.a. e più di recente dalle ricerche di P. Marti (1991) e J. Schlaich (1991) dell'Università di Stoccarda, che ne hanno esteso l'utilizzo agli elementi tozzi in c.a.
Il metodo STM rientra nei metodi di analisi plastica delle strutture e si basa sull'applicazione del primo teorema dell'analisi limite: il teorema statico o del limite inferiore. Il procedimento operativo consiste nell'individuare un meccanismo di trasferimento dello sforzo, mediante un traliccio costituito da puntoni (strut), tiranti (tie) e nodi. Dall'imposizione dell'equilibrio si ricavano gli sforzi (di compressione e trazione) agenti negli elementi e nei nodi. Noti gli sforzi, si dimensionano le sezioni di calcestruzzo e le aree di armatura in maniera da rispettare i limiti di resistenza dei materiali, assicurando così l'ammissibilità statica degli sforzi interni. In queste condizioni è applicabile il teorema statico dell'analisi limite, che fornisce la giustificazione teorica del metodo ed assicura che il carico massimo associato al traliccio considerato rappresenta una stima in difetto (un limite inferiore) del carico di collasso.
In un determinato contesto applicativo è in genere possibile identificare più di un modello STM, capace di rispettare l'equilibrio e il rispetto della frontiera plastica dei materiali. In questi casi si otterranno stime diverse per il carico di collasso, ma in ogni caso a vantaggio di statica. Questa osservazione può in effetti essere usata anche per raffinare il modello per ottenere valori che meglio approssimano il carico di collasso del sistema.
In questa versione del programma sono state sviluppate funzioni di progetto e verifica che sfruttano la potenza del metodo STM per il progetto del pozzetto, da preferire in linea generale alle vecchie norme Cnr in quanto espressione autorevole di una linea di ricerca ormai affermata, riconosciuta in codici con valenza internazionale come l'EC2.
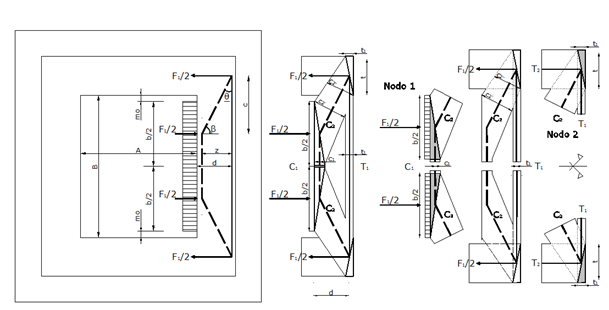
In figura, lo schema “strut & tie” per il progetto del colletto nel plinto a bicchiere
Effetto cinematico sismico per i pali
Una novità molto interessante della nuova versione è l'introduzione dell'effetto cinematico per i pali, che valuta l'incremento di sollecitazione che interessa il palo per effetto dell'interazione fra palo e terreno, in presenza di moto sismico. Intuitivamente tali effetti corrispondono a quelli che si avrebbero in un palo privo di sovrastuttura, immerso nel terreno, per effetto della propagazione verticale nel sottosuolo di onde di taglio. Il fenomeno dipende in maniera complessa dalla stratigrafia, dal comportamento non lineare del terreno, dagli effetti di smorzamento collegati e dall'entità delle deformazioni indotte dal sisma. In letteratura sono stati pubblicati svariati studi sull'argomento, nei quali sono state predisposte complesse modellazioni dinamiche agli elementi finiti, in campo lineare e non lineare. Essenzialmente però l'obiettivo rimane quello di tarare metodi semplificati in grado di quantificare l'effetto con una accuratezza sufficiente ai fini tecnici, considerato che un approccio rigoroso non è allo stato attuale proponibile al di fuori dell'ambiente accademico. In genere, si è visto che in linea generale l'effetto cinematico è trascurabile rispetto all'effetto inerziale, ovvero all'effetto dovuto all'oscillazione della sovrastruttura, a meno che non ci si trovi in circostanze particolari che tendono ad amplificare il fenomeno, quali ad esempio la presenza di un forte contrasto di rigidezza fra due strati di terreno successivi, una forte sismicità del sito, una classe di sottosuolo D o peggiore. La stessa normativa italiana (§7.11.5.3.2 .Ntc08/Ntc18) raccomanda che in queste condizioni, in costruzioni di classe d'uso importante (III) o strategica (IV) sia opportuno valutare gli effetti dovuti all'interazione cinematica, sovrapponendoli a quelli inerziali.
Per soddisfare questa esigenza, nel presente aggiornamento sono stati implementati due dei più diffusi metodi semplificati per la valutazione dell'effetto cinematico:
· il metodo di Dobry R., O’Rourke
· il metodo di Nikolaou et al.
Entrambi i metodi consentono di ottenere il momento massimo M nel palo all'interfaccia fra due strati di diversa rigidezza, che sono individuati da programma in base al maggiore contrasto di rigidezza fra i moduli G del terreno. Una volta ottenuto il valore puntuale massimo, l'effetto è propagato ai fini delle verifiche su tutta la luce del palo, supponendo che il diagramma dei momenti sia espresso da una legge cubica e imponendo per esso il valore nullo alla punta del palo e una aliquota prefissata in testa al palo.
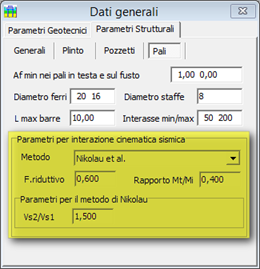
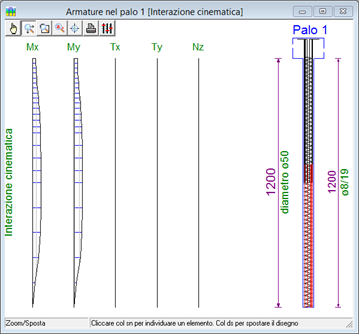
Nel Foglio Dati Generali il quadro parametri dell'interazione cinematica. Nel Foglio delle armature i diagrammi del momento dovuti a tale effetto.
Carico limite orizzontale di un palo con la teoria di Broms
Nella nuova versione è adesso possibile valutare la portanza dei pali a carico orizzontale secondo la teoria di Broms, che rientra nei procedimenti tipici dell'analisi limite e si basa sull'applicazione dei teoremi cinematico e statico. Il primo è applicabile a schemi cinematicamente compatibili e porta a stime in eccesso del carico di collasso, il secondo è invece applicabile a schemi staticamente ammissibili e porta a stime in difetto.
La procedura che è stata implementata nel programma consiste nel considerare per l'insieme palo-terreno uno schema di calcolo cinematicamente compatibile, dal quale si ottiene per l'imposizione dell'equilibrio una stima in eccesso del carico limite. Si valuta quindi il massimo momento nel palo M e si controlla che in nessun punto sia violato il limite plastico, ovvero che il momento massimo agente non ecceda il momento plastico resistente My. Se quest'ultima condizione è rispettata, allora lo schema considerato sarà anche staticamente ammissibile e il corrispondente carico in testa al palo, essendo contemporaneamente un limite superiore (per il teorema cinematico) ed un limite inferiore (per il teorema statico), coinciderà col valore limite. Se non lo fosse, si assume che nel punto di massimo momento si formi una cerniera plastica e si ripete il procedimento.
Nelle seguenti figure sono mostrati i meccanismi di calcolo del carico limite orizzontale in cui si può articolare la procedura di analisi, nell'ipotesi di palo incastrato in testa:
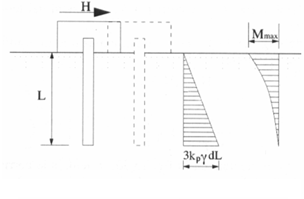
Meccanismo di palo corto
Il palo è considerato rigido ed è assoggettato ad una traslazione uniforme: il diagramma delle tensioni orizzontali è triangolare e il massimo momento è attinto nella sezione di testa.
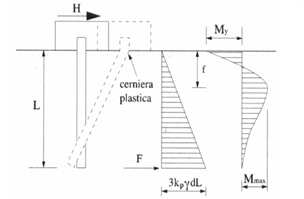
Meccanismo di palo intermedio
Il palo ha una cerniera plastica in testa ed è assoggettato ad una rotazione intorno ad un polo vicino alla punta, il diagramma delle tensioni orizzontali è triangolare e il massimo momento è attinto in un punto intermedio lungo il fusto.
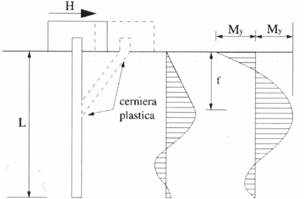
Meccanismo di palo lungo
Il palo ha due cerniere plastiche, una in testa e l'altra nel punto di momento massimo del passo precedente, ed è assoggettato ad una rotazione intorno alla seconda cerniera, il diagramma delle tensioni orizzontali è triangolare nel tratto fra le due cerniere.
Nuove procedure di calcolo per i cedimenti
Nuove funzionalità sono state introdotte per la verifica dei cedimenti, queste prevedono adesso la segnalazione dei casi non soddisfatti, mediante messaggi di avvertimento a video e con l'evidenziazione in griglia dei valori che eccedono la soglia assegnata dall'utente. Inoltre, le modalità di calcolo si arricchiscono di un altro metodo di calcolo (Bowles), per cui le opzioni disponibili sono ora:
· il metodo del semispazio elastico,
· il metodo di Bowles,
applicabili sia per il caso di plinto superficiale, sia per il plinto su pali.
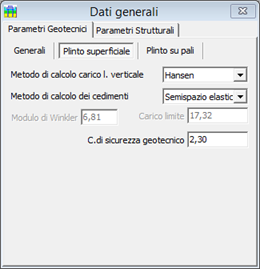
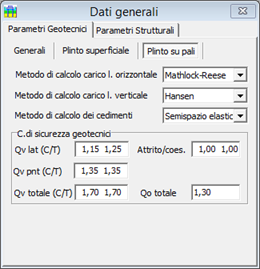
In figura vediamo il pannello dei parametri geotecnici per il caso di plinto superficiale e su pali che contiene
anche la selezione dei metodi di calcolo per la portanza verticale, orizzontale e per il calcolo dei cedimenti.
Verifica dello scorrimento in fondazione
Le verifiche di tipo geotecnico si arricchiscono inoltre della verifica dello scorrimento all'intradosso del plinto. L'attuale normativa dispone, infatti, che per i plinti superficiali vengano presi in considerazione i meccanismi di collasso per scorrimento sul piano di posa per gli stati limite ultimi di tipo geotecnico (§6.4.2.1 Ntc18). Per i plinti su pali c'è una esigenza analoga in quanto si richiede la verifica dei meccanismi di collasso per carico limite della palificata nei riguardi dei carichi trasversali (§6.4.3.1 Ntc18). In entrambi i casi, la verifica viene effettuata secondo la combinazione di fattori parziali indicata simbolicamente come A1+M1+R3 prevista dall'Approccio 2, in cui R3 è il fattore di sicurezza sulla resistenza globale.
Lo scorrimento orizzontale di una fondazione rispetto al terreno avviene nel momento in cui le componenti delle forze agenti orizzontali prevalgono le forze che si oppongono a tale movimento. Nel caso di plinto superficiale queste forze sono dovute all'attrito e all'adesione agente sull'interfaccia terreno-fondazione e, qualora fosse presente, la spinta passiva laterale sulle superfici verticali controterra. Nel caso di plinto su pali, le forze resistenti allo scorrimento sono rappresentate dalla sommatoria dei contributi resistenti dei pali, valutabili per ogni palo come valore minimo fra la portanza laterale del palo (calcolata secondo Broms) e la resistenza a taglio nella sezione di testa.


La griglia risultati della verifica a scorrimento per il plinto superficiale e su pali.
Nell'ultima colonna è riportato il fattore d'impegno (minore di uno per verifica soddisfatta).
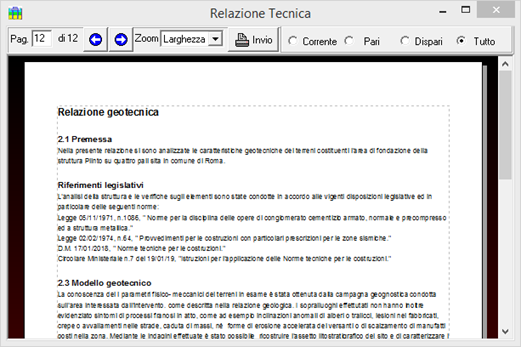
Redazione della relazione geotecnica di base e della relazione sulle fondazioni
La relazione geotecnica è un elaborato tecnico espressamente richiesto dalla normativa (Ntc08/Ntc18 p. 6.1.2), nel quale devono essere illustrati tutti gli aspetti di tipo geotecnico che intervengono nel progetto: le scelte progettuali, il programma e i risultati delle indagini, la caratterizzazione e la modellazione geotecnica, le analisi per il dimensionamento geotecnico delle opere e la descrizione delle fasi e delle modalità costruttive.
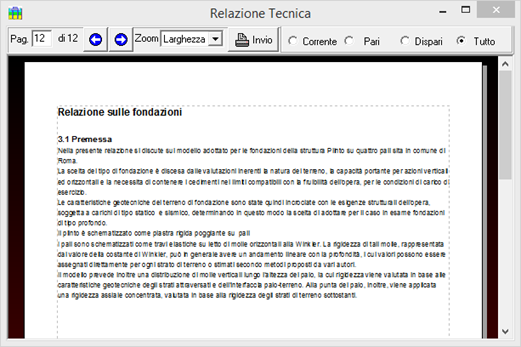
Nella nuova versione del programma, la disponibilità di contenuti geotecnici riguardanti la stima della portanza limite (verticale ed orizzontale), del calcolo dei cedimenti in fondazione e della verifica di scorrimento ha reso possibile la redazione della relazione geotecnica, sia pure in una forma suscettibile di conferma ed arricchimento da parte dell'utente, che potrà integrarne i contenuti in base ad informazioni di maggiore dettaglio.